GrowthMaps.jl

GrowthMaps

GrowthMaps.jl produces gridded population level growth rates from environmental data, and fitted growth and stress models, following the method outlined in Maino et al, "Forecasting the potential distribution of the invasive vegetable leafminer using ‘top-down’ and ‘bottom-up’ models" (in press).

GrowthMaps.jl is an alternative to CLIMEX and similar tools. Its key point of differentiation from other methods is that results arrays have units of growth/time. Another useful property of these models is that growth rate layers can be added and combined arbitrarily.

A primary use-case for GrowthMaps layers is in for calculating growth-rates for . This allows heterogeneous organism growth rates to influence dispersal patterns, simulating permanent range limits and potential for seasonal range shift.

For data input, this package leverages GeoData.jl to import datasets from many different sources. Files are loaded lazily in sequence to minimise memory, using the GeoSeries abstraction, that can hold "SMAP" HDF5 files, NetCDFs, or GeoStacks of tif or other GDAL source files, or simply memory-backed arrays. These data sources can be used interchangeably.

Computations can be run on GPUs, for example with arraytype=CuArray to use CUDA for Nvidia GPUs.

Example

Here we run a single growth model over SMAP data, on a Nvida GPU:

using GrowthMaps, GeoData, HDF5, CUDA, Unitful

# Define a growth model
p = 3e-01
ΔH_A = 3e4cal/mol
ΔH_L = -1e5cal/mol
ΔH_H = 3e5cal/mol
Thalf_L = 2e2K
Thalf_H = 3e2K
T_ref = K(25.0°C)
growthmodel = SchoolfieldIntrinsicGrowth(p, ΔH_A, ΔH_L, Thalf_L, ΔH_H, Thalf_H, T_ref)

# Wrap the model with a data layer with the key
# to retreive the data from, and the Unitful.jl units.
growth = Layer(:surface_temp, K, growthmodel)

Now we will use GeoData.jl to load a series of SMAP files lazily, and GrowthMaps.jl will load them to the GPU just in time for processing:

# Load 1000s of HDF5 files lazily using GeoData.jl
series = SMAPseries("your_SMAP_folder")

# Run the model
output = mapgrowth(growth;
    series=series,
    tspan=DateTime(2016, 1):Month(1):DateTime(2016, 12),
    arraytype=CuArray, # Use an Nvidia GPU for computations
)

# Plot every third month of 2016:
output[Ti(1:3:12)] |> plot

GrowthMaps.jl is fast.

As a rough benchmark, running a model using 3 3800*1600 layers from 3000 SMAP files on a M.2. drive takes under 7 minutes on a desktop with a good GPU, like a GeForce 1080. The computation time is trivial, running ten similar models takes essentially the same time as running one model. On a CPU, model run-time becomes more of a factor, but is still fast for a single model.

See the Examples section in the documentation to get started. You can also work through the example.jmd in atom (with the language-weave plugin) or the notebook.

Live Interfaces

GrowthMaps provides interfaces for manually fitting models where automated fits are not appropriate.

Model curves can be fitted to an AbstractRange of input data using manualfit:

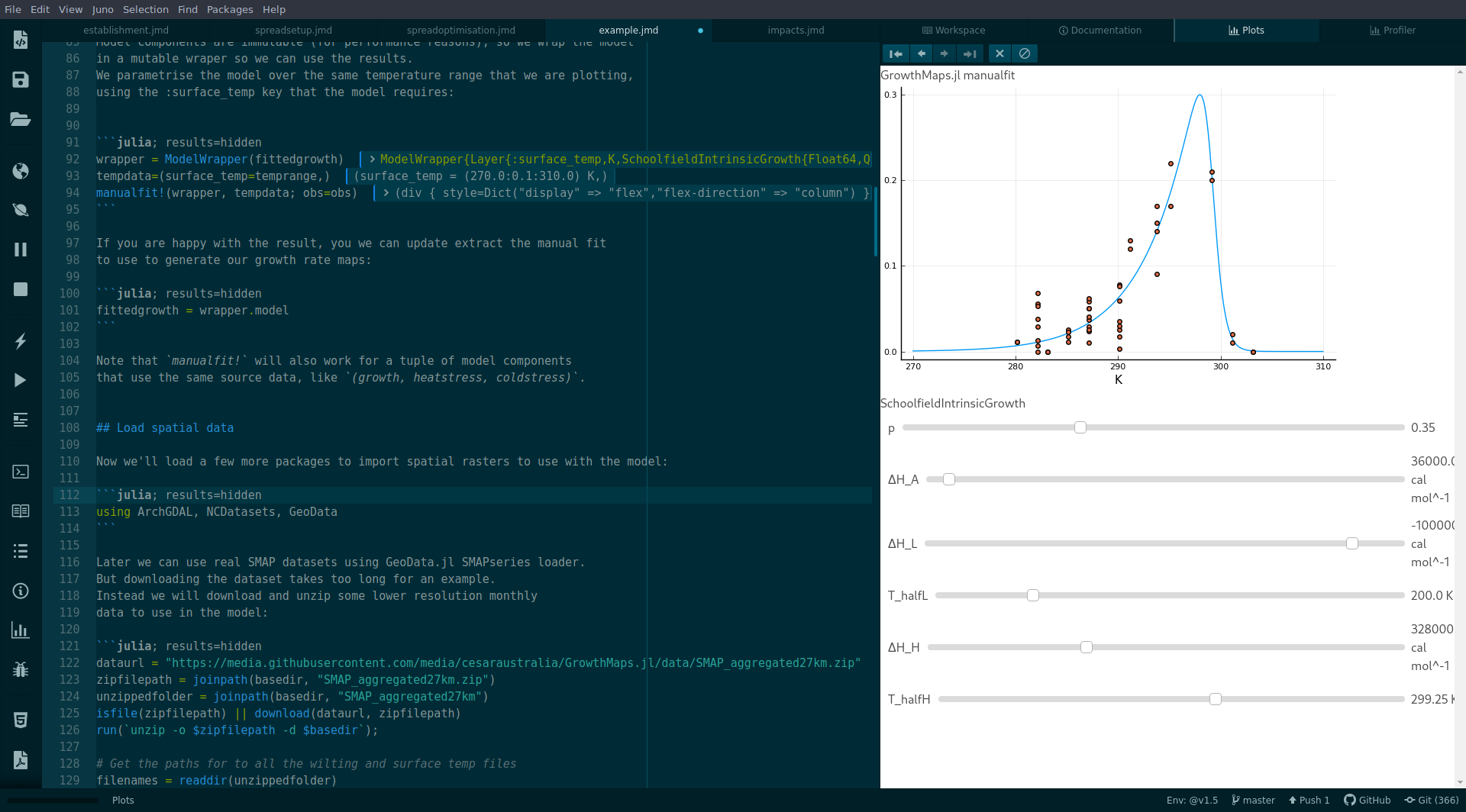
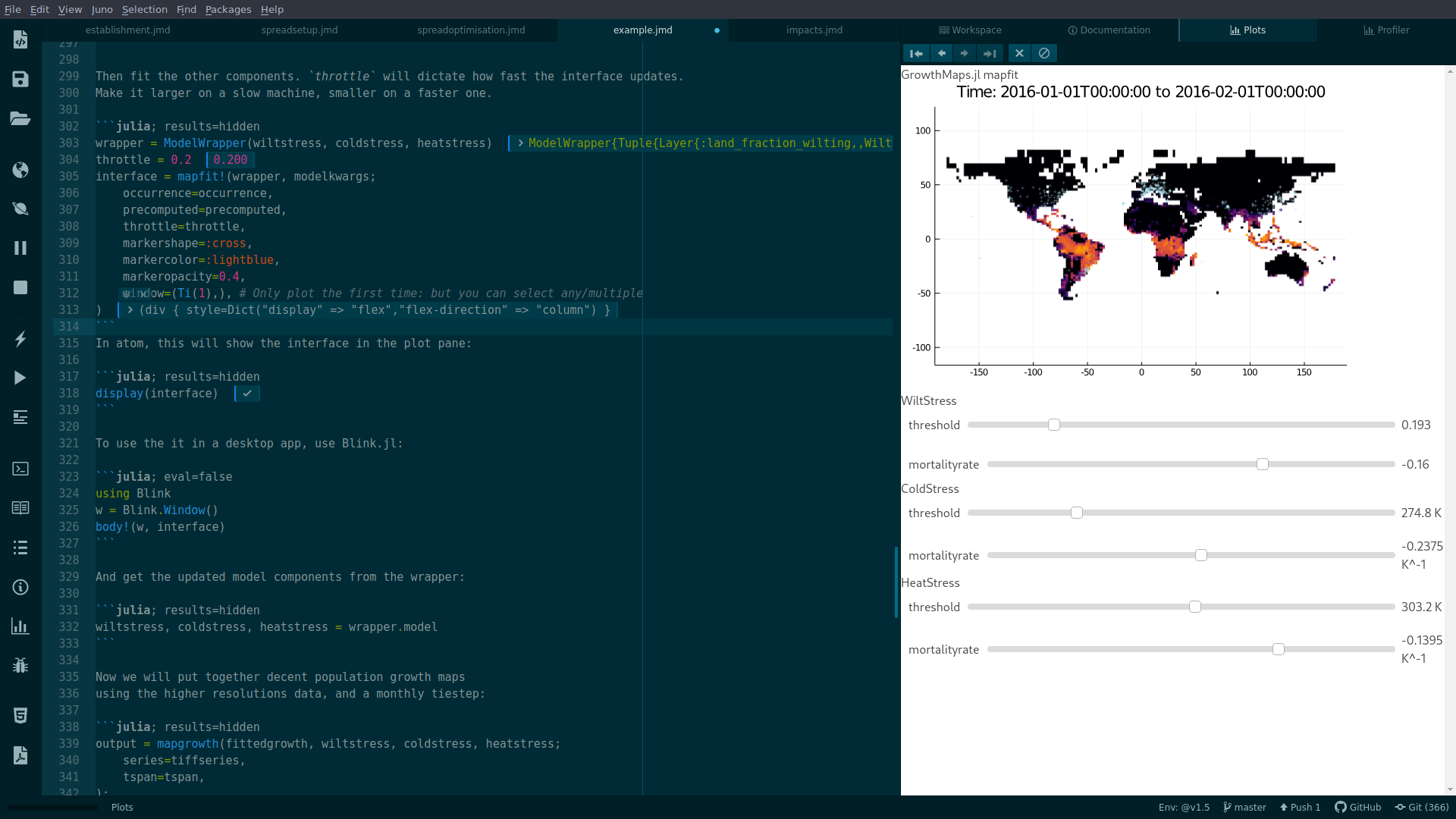
Observations can be fitted to a map. Aggregated maps GeoSeries can be used to fit models in real-time. See the examples for details.

The intrinsic rate of population growth is the exponential growth rate of a population when growth is not limited by density dependent factors.

More formally, if the change in population size $N$ with time $t$ is expressed as $\frac{dN}{dt} = rN$, then $r$ is the intrinsic population growth rate (individuals per day per individual) which can be decomposed into per capita reproduction and mortality rate. The intrinsic growth rate parameter $r$ depends strongly on temperature, with population growth inhibited at low and high temperatures.

This can be described using a variety of non-linear functions, see SchoolfieldIntrinsicGrowth for an implementation.

Layer{K,U}(model::RateModel)
Layer(key::Symbol, model::RateModel)
Layer(key::Symbol, u::Union{Units,Quantity}, model::RateModel)

Layers connect a model to a data source, providing the key to look up the layer in a Rasters.jl RasterStack, and specifying the scientific units of the layer, if it has units. Using units adds an extra degree of safety to your calculation, and allows for using data in different units with the same models.

LowerStress(key::Symbol, threshold, mortalityrate)

A StressModel where stress occurs below a threshold at a specified mortalityrate for some environmental layer key.

If units are used, the Layer that wraps this models must be in units convertible to the units used in threshold.

A RateModel contains the parameters to calculate the contribution of a growth or stress factor to the overall population growth rate.

A rate method corresponding to the model type must be defined specifying the formulation, and optionally a condition method to e.g. ignore data below thresholds.

Returns

An AbstractFloat with implicit units of N*N^-1*T^-1, where N is the number of individuals and T is time, usually one day.

It should not return a Unitful.jl Quantity.

SchoolfieldIntrinsicGrowth(p, ΔHA, ΔHL, ΔHH, ThalfL, ThalfH, Tref, R)

A GrowthModel where the temperature response of positive growth rate is modelled following Schoolfield et al. 1981, "Non-linear regression of biological temperature-dependent rate models base on absolute reaction-rate theory".

Arguments

• p::P: growth rate at reference temperature T_ref
• ΔH_A: enthalpy of activation of the reaction that is catalyzed by the enzyme, in cal/mol or J/mol.
• ΔH_L: change in enthalpy associated with low temperature inactivation of the enzyme.
• ΔH_H: change in enthalpy associated with high temperature inactivation of the enzyme.
• T_halfL: temperature (Unitful K) at which the enzyme is 1/2 active and 1/2 low temperature inactive.
• T_halfH: temperature (Unitful K) at which the enzyme is 1/2 active and 1/2 high temperature inactive.
• T_ref: Reference temperature in kelvin.

This can be parameterised from empirical data, (see Zhang et al. 2000; Haghani et al. 2006; Chien and Chang 2007) and non-linear least squares regression.

Extreme stressor mortality can be assumed to occur once an environmental variable $s$ exceeds some threshold (e.g. critical thermal maximum), beyond which the mortality rate scales approximately linearly with the depth of the stressor.

Stressor induced mortality is incorporated in growth rates by quantifying the threshold parameter $s_c$ beyond which stress associated mortality commences, and the mortalityrate parameter $m_s$ which reflects the per-capita mortality per stress unit, per time (e.g. degrees beyond the stress threshold per day).

When stressors are combined in a model, the mortality rate for each stressor $s$ is incorporated as $\frac{dN}{dt}=(r_p-r_n)N$ where $r_n = \sum{s}f(s, c_s)m_s$ and $f(s, c_s)$ is a function that provides the positive units by which s exceeds $s_c$.

This relies on the simplifying assumption that different stressors contribute additively to mortality rate, but conveniently allows the mortality response of stressors to be partitioned and calculated separately to the intrinsic growth rate, which aids parameterisation and modularity. More complicated stress responses are more likely to capture reality more completely, but the availability of data on detailed mortality responses to climatic stressors is often lacking.

Upper and lower stresses may be in relation to any environmental variable, specied with the key parameter, that will use the data at that key in RasterStack for the current timestep.

UpperStress(key::Symbol, threshold, mortalityrate)

A StressModel where stress occurs above a threshold at the specified mortalityrate, for some environmental layer key.

condition(m::RateModel, x)

Subset the data before applying the rate method, given the model m and the environmental variable of value x.

Returns a Bool. true will run the rate model, false will keep the current growth rate, which is 1 for a single model.

If not defined for a given RateModel, condition returns true for all cells.

condition methods should use the @inline macro to force inlining.

fit!(model, obs::AbstractArray)

Fit a model to data with least squares regression, using curve_fit from LsqFit.jl. The passed in model should be initialised with sensible defaults, these will be used as the initial parameters for the optimization.

Any (nested) Real fields on the struct are flattened to a parameter vector using Flatten.jl. Fields can be marked to ignore using the @flattenable macro from FieldMetadata.jl.

Arguments

• model: Any constructed RateModel or a Tuple of RateModel.
• obs: A Vector of (val, rate) tuples where val is the value of the x-axis variable (such as temperature), and rate is the growth rate observed.

Returns

An updated Model containing the fitted parameter values.

manualfit!(model::Model, data::NamedTuple; obs=[], kw...) =

Returns the fitted model.

Arguments

• obs: A Vector of (val, rate) tuples where val is the value of the x-axis variable (such as temperature), and rate is the growth rate observed.
• data: A NamedTuple of AbstractVector. The NamedTuple key/s must match the key required by the Layer/s.
• obs: Optional observations to scatter-plot over the curve. A Vector of (val, rate) tuples where val is the value of the x-axis variable (such as temperature), and rate is the growth rate observed.
• kwargs: passed to plot

Example

p = 3e-01
ΔH_A = 3e4cal/mol
ΔH_L = -1e5cal/mol
ΔH_H = 3e5cal/mol
Thalf_L = 2e2K
Thalf_H = 3e2K
T_ref = K(25.0°C)
growthmodel = SchoolfieldIntrinsicGrowth(p, ΔH_A, ΔH_L, Thalf_L, ΔH_H, Thalf_H, T_ref)
model = Model(Layer(:surface_temp, K, growthmodel))
obs = []

tempdata=(surface_temp=(270.0:0.1:310.0)K,)
manualfit!(model, tempdata; obs=obs)

To use the interface in a desktop app, use Blink.jl:

julia; eval=false using Blink w = Blink.Window() body!(w, interface) ```

mapfit!(model::Model, modelkwargs;
        occurrence=[],
        precomputed=nothing,
        throttle=0.1,
        window=(Band(1),),
        kwargs...
)

Fit a model to the map.

Arguments

• occurence: a Vector of occurence locations, as (lon, lat) tuples.
• modelkwargs: are passed to the mapgrowth with the model.
• mapkwargs: are passed to the plot function the plots the Raster
• throttle: the response time of Interact.jl sliders.
• window: selects a window of the output to plot. By default this is (Band(1),), which just removes the Band dimension from a Raster, if it exists.
• kwargs: passed to Plots.scatter!

Example

model = Model(wiltstress, coldstress, heatstress)
interface = mapfit!(model, modelkwargs;
    occurrence=occurrence,
    precomputed=precomputed,
    throttle=0.2,
    window=(Band(1),),
    markershape=:cross,
    markercolor=:lightblue,
    markeropacity=0.4
)
display(interface)

To use the interface in a desktop app, use Blink.jl:

using Blink
w = Blink.Window()
body!(w, interface)

mapgrowth(model; series::AbstractRasterSeries, tspan::AbstractRange)
mapgrowth(layers...; kwargs...)

Combine growth rates accross layers and subperiods for all required periods.

Arguments

• model: A Model, NamedTuple of Model, or Tuple of Layer components.

Layers can also be passed in as separate arguments. A NamedTuple of models will all be run from the same data source, reducing load time.

Keyword Arguments

• series: any AbstractRasterSeries from Rasters.jl
• tspan: AbstractRange for the timespan to run the layers for. This will become the index values of the output Raster time-dimension Ti.

The output is a Raster with the same dimensions as the passed in stack layers, and a Time dimension with a length of nperiods.

rate(m::RateModel, x)

Returns a growth rate multiplier for a model given environmental variable x, for a single cell. Must be defined for all RateModel.

Arguments

• m: the object containing the model parameters
• x: the value at a particular location for of an environmental variable specified by the models key() method, using corresponding to its key field.

rate methods should use the @inline macro to force inlining.