Dispersal.jl

Dispersal

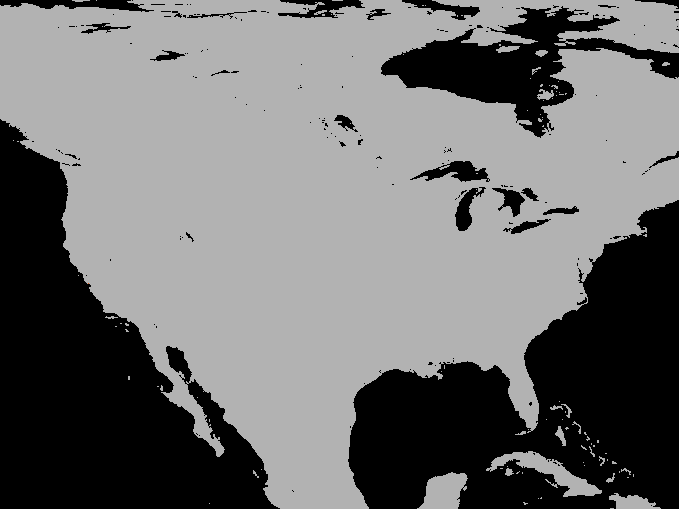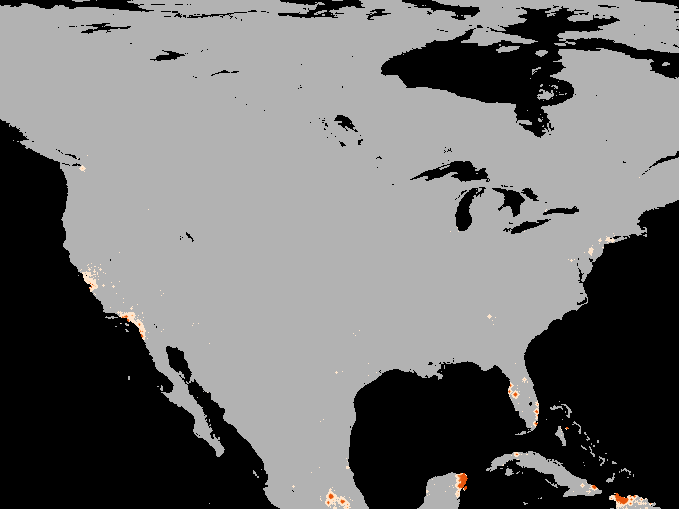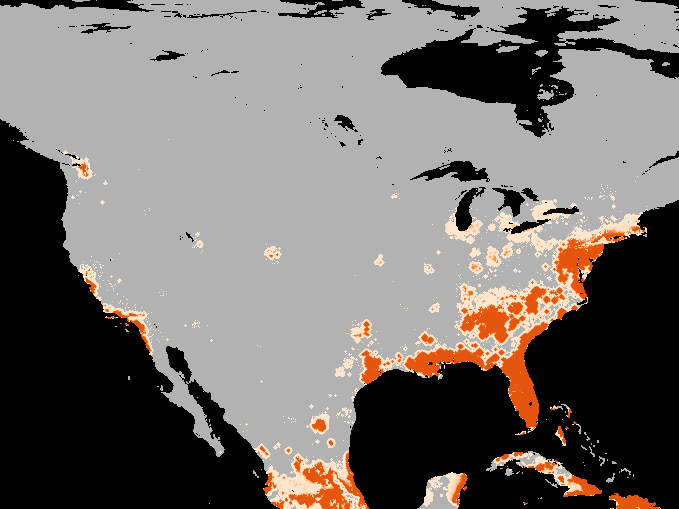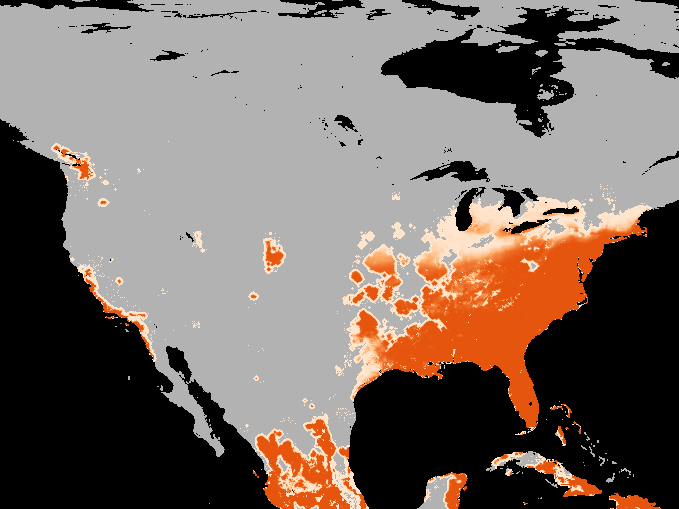
A simulation of the spotted-wing drosophola invasion of the continental United States as detailed in Maino, Schouten, and Umina (2021)

Dispersal.jl extends DynamicGrids.jl to provide model components and tools for grid-based simulations of organism dispersal.

Growth rates, dispersal kernels, Allee effects, and randomised jump and human assisted dispersal rules are provided. These components can be combined into complex dispersal models. Custom rules can easily added and combined with the provided set. See the documentation for examples and the lists of included rules.

DynamicGridsInteract provides an interactive interface for atom and jupyter notbooks (InteractOuput), desktop (ElectronOutput) and online web applications (ServerOuput), where complete models, including your custom rules, can be manipulated during live simulations.

DynamicGridsGtk provides GtkOutput for a simple graphical viewer.

GrowthMaps.jl can efficiently generate summarised raster data for vital rates (e.g. intrinsic growth rates) based on higher resolution and shorter interval environmental data.

GrowthRule <: CellRule

Abstract supertype for growth dynamics rules.

ExponentialGrowth <: CellRule

ExponentialGrowth(; rate, timestep, [nsteps_type])
ExponentialGrowth{R}(; rate, timestep, [nsteps_type])
ExponentialGrowth{R,W}(; rate, timestep, [nsteps_type])

Exponential growth of population size N based on an intrinsic growth rate $r$, using the exact solution between timesteps $t$ and $t-1$:

\[N_t = N_{t-1}e^{r t}\]

Keywords

• rate: Intrinsic growth rate. May be a Number, an Aux array or another Grid.
• timestep: Time step for the growth rate calculation, in a type compatible with the simulation tspan.
• nsteps_type: Specify the floating point type to use when nsteps is generated from the timestep, if it is required for type-stability or performance. The default is Float64.

Pass grid Symbols to R or both R and W type parameters to use to specific grids.

LogisticGrowth <: GrowthRule

LogisticGrowth(; rate, carrycap, timestep, [nsteps_type])
LogisticGrowth{R}(; rate, carrycap, timestep, [nsteps_type])
LogisticGrowth{R,W}(; rate, carrycap, timestep, [nsteps_type])

Logistic growth rate of population size $N$ based on an intrinsic growth rate $r$ and carry capacity $K$, using the exact solution between timesteps $t+1$ and $t$:

\[N_{t+1} = (N_t K) / (N_t + (K - N_t) e^{-rt})\]

Saturation only applies with positive growth.

Keywords

These may be a Number, an Aux array or another Grid:

• rate: Intrinsic growth rate.
• carrycap: Carrying capacity.
• timestep: Time step for the growth rate, in a type compatible with the simulation tspan.
• nsteps_type: Specify the floating point type to use when nsteps is generated from the timestep, if it is required for type-stability or performance. The default is Float64.

Pass grid Symbols to R or both R and W type parameters to use to specific grids.

ThresholdGrowth <: CellRule

ThresholdGrowth(; rate, threshold)
ThresholdGrowth{R}(; rate, threshold)
ThresholdGrowth{R,W}(; rate, threshold)

Simple threshold mask. Values below a certain threshold are replaced with zero.

Keywords

These may be a Number, an Aux array or another Grid.

• rate: Intrinsic growth rate.
• threshold: Minimum viability threshold below which population falls to zero.

Pass grid Symbols to R or both R and W type parameters to use to specific grids.

Mortality <: CellRule

Abstract super type for rules of survival effect For best performance these should be chained with other CellRule or following an NeighborhoodRule.

ExponentialMortality <: Mortality

ExponentialMortality(; rate, threshold, timestep, [nsteps_type])
ExponentialMortality{R}(; rate, threshold, timestep, [nsteps_type])
ExponentialMortality{R,W}(; rate, threshold, timestep, [nsteps_type])

Exponential mortality based on exposure threshold and mortality rate parameter, using exact solution.

Exponential mortality based on exposure grid $X$, an exposure threshold parameter $z$ and a mortality rate $r$ using exact solution between time $t$ and `$t+1$:

\[N_{t+1} = N_{t}e^{-r t(X-z)}\]

Keywords

• rate: Mortality rate.
• threshold: Exposure threshold under which there is no effect.
• timestep: Time step for the growth rate, in a type compatible with the simulation tspan.
• nsteps_type: Specify the floating point type to use when nsteps is generated from the timestep, if it is required for type-stability or performance. The default is Float64.

rate and threshold can be a Number, an Aux array or another Grid`.

Pass grid Symbols to R or both R and W type parameters to use to specific grids. R is a 2 Grids NamedTuple like Tuple{:population,:exposure} and W return only the first grid :population.

LoglogisticMortality <: Mortality

LoglogisticMortality(; median, hillcoefficient, timestep, [nsteps_type])
LoglogisticMortality{R}(; median, hillcoefficient, timestep, [nsteps_type])
LoglogisticMortality{R,W}(; median, hillcoefficient, timestep, [nsteps_type])

Loglogistic mortality based on median, $α$ and hill coefficient $β$.

Cumulative function of loglogistic:

\[F(x; α, β) = x^β/(α^β + x^β)\]

where $α>0$ is the scale and $β>0$ is the shape.

Keywords

• median: Median of the loglogistic function
• hillcoefficient: Hill's coefficient, a measure of ultrasensitivity (i.e. how steep is the response curve). May be a Number, an Aux array or another Grid.
• timestep: Time step for the mortality rate, in a type compatible with the simulation tspan.

Pass grid Symbols to R or both R and W type parameters to use to specific grids. R is a 2 Grids NamedTuple like Tuple{:population,:exposure} and W return only the first grid :population.

AlleeExtinction <: CellRule

AlleeExtinction(minfounders)
AlleeExtinction{R}(; minfounders=5.0)
AlleeExtinction{R,W}(minfounders)

Causes extinction in a cell when a population is below a minimum number of individuals.

• minfounders: minimum founding individuals required for a viable population. Must be a type that can be compared to the grid values using isless.

Pass grid Symbols to R or both R and W type parameters to use to specific grids.

InwardsPopulationDispersal <: NeighborhoodRule

InwardsPopulationDispersal(; kw...)
InwardsPopulationDispersal{R}(; kw...)
InwardsPopulationDispersal{R,W}(; kw...)

Implements deterministic dispersal from populations in neighboring cells to the current cell.

The result should be identical to those obtained substituting InwardsDispersal for OutwardsDispersal but will perform better when populations are spread across the grid.

Keywords

• neighborhood: Any DynamicGrids.jl Neighborhood, or an already constructed DispersalKernel. Using this keyword means radius is ignored, and for a DispersalKernel, all other keywords are ignored.
• neighborhood: Neighborhood object specifying the range from the origin of the discretised dispersal kernal. Defaults to Window(radius).
• formulation: kernel formulation object holding the exact form of the kernal. Default ExponentialKernel.
• cellsize: the cell size of the discretised kernal (i.e. simulation grid size). Default is 1.0.
• distancemethod: DistanceMethod object for calculating distance between cells. The default is CentroidToCentroid.

Pass grid Symbols to R or both R and W type parameters to use to specific grids.

OutwardsPopulationDispersal <: SetNeighborhoodRule

OutwardsPopulationDispersal(; kw...)
OutwardsPopulationDispersal{R}(; kw...)
OutwardsPopulationDispersal{R,W}(; kw...)

Implements deterministic dispersal from the current cell to populations in neighboring cells.

This will make sense ecologically where cell populations are large, otherwise a randomised kernel may be more suitable.

The result should be identical to those obtained substituting OutwardsDispersal for InwardsDispersal but may be more efficient when a small number of cells are occupied. Conversely, it will become less efficient when a large proportion of the grid is occupied.

Keywords

• neighborhood: Any DynamicGrids.jl Neighborhood, or an already constructed DispersalKernel. Using this keyword means radius is ignored, and for a DispersalKernel, all other keywords are ignored.
• neighborhood: Neighborhood object specifying the range from the origin of the discretised dispersal kernal. Defaults to Window(radius).
• formulation: kernel formulation object holding the exact form of the kernal. Default ExponentialKernel.
• cellsize: the cell size of the discretised kernal (i.e. simulation grid size). Default is 1.0.
• distancemethod: DistanceMethod object for calculating distance between cells. The default is CentroidToCentroid.

Pass grid name Symbols to R and W type parameters to use specific grids.

DispersalKernel <: AbstractKernelNeighborhood

DispersalKernel(; kw...)

Dispersal kernel for taking the dot product of the neighborhood and a matching kernel of weights. May hold any Neighborhood object: the kernel will be built to match the shape, using the folumation, cellsize and distancemethod.

Keyword Arguments

• neighborhood: Any DynamicGrids.jl Neighborhood, or an already constructed DispersalKernel. Using this keyword means radius is ignored, and for a DispersalKernel, all other keywords are ignored.
• neighborhood: Neighborhood object specifying the range from the origin of the discretised dispersal kernal. Defaults to Window(radius).
• formulation: kernel formulation object holding the exact form of the kernal. Default ExponentialKernel.
• cellsize: the cell size of the discretised kernal (i.e. simulation grid size). Default is 1.0.
• distancemethod: DistanceMethod object for calculating distance between cells. The default is CentroidToCentroid.

abstract type KernelFormulation

KernelFormulation

Abstract supertype for functors that calculate the probability density based on distance.

Concrete implementations must define functor methods with the form:

(k::SomeKernel)(distance) = # do something with `distance` and `k`"

Using an anonymous function would not allow rebuildable model parameters.

ExponentialKernel <: KernelFormulation

ExponentialKernel(λ)

Probability density function of distance $d$.

\[y = e^{-d/λ}\]

where λ is a shape parameter.

GeometricKernel <: KernelFormulation

GeometricKernel(α)

Probability density function of distance $d$.

The Geometric kernel has a power-law decrease.

\[y = (1+d)^α (α+1)(α+2) / (2 π)\]

where α is a shape parameter.

GaussianKernel <: KernelFormulation

GaussianKernel(α)

Probability density function of distance $d$.

\[y = 1/ (π α^2) e^{-d^2/α^2} \]

where α is a positive parameter.

WeibullKernel <: KernelFormulation

WeibullKernel(α,β)

Probability density function of distance $d$.

\[y =β /(2 π α^2) d^{β-2} e^{ -d^β/α^β} \]

where α and β are positive parameters.

abstract type DistanceMethod

DistanceMethod

Abstract supertype for methods of calculating distances and discretised dispersal probabilities between cells in a grid. between cells in a grid.

Distance calculation methods include:

• CentroidToCentroid
• AreaToArea
• AreaToCentroid

Which are adapted from: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"

The CentroidToArea method has not been implemented.

struct CentroidToCentroid <: DistanceMethod

CentroidToCentroid <: DistanceMethod

CentroidToCentroid()

Calculates the discrete probability of dispersal between source and destination cell centroids. This is the naive method, but it will not handle low grid resolution well due to severe truncation.

See: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"

AreaToCentroid <: DistanceMethod

AreaToCentroid(subsampling)
AreaToCentroid(; subsampling=10.0)

Calculates the discrete probability of dispersal between source cell area and destination centroid.

See: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"

AreaToArea <: DistanceMethod

AreaToArea(subsampling)
AreaToArea(; subsampling=10.0)

Calculates the discrete probability of dispersal between source and destination based on cell areas.

See: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"

JumpDispersal <: SetCellRule

JumpDispersal(; prob_threshold, spotrange)
JumpDispersal{R}(; prob_threshold, spotrange)
JumpDispersal{R,W}(; prob_threshold, spotrange)

Jump dispersal simulates a random long distance dispersal event, which occurs at a given probablity. A random cell within the spotrange is invaded by duplicating the entire population of the source cell at the destination cell.

Keyword Arguments

• prob_threshold: probability of dispersal, between one and zero. May be a Number, an Aux array or another Grid:
• spotrange: number of cells in range of jumps, in any direction.

Pass grid Symbols to R or both R and W type parameters to use to specific grids.

HumanDispersal <: SetCellRule

HumanDispersal{R,W}(; kw...)

Implements human-driven dispersal patterns using population density data.

The number of long-distance migrants from an origin is set proportional to the level of human population with the coefficient dispersalperpop. The destination of long-distance migration is is calculated by using the distance $d$ between and human population $H$ at origin cell $i$ and destination cell $j$ through a simple gravity function:

\[g_{i,j} = (H_i H_j)^β/(d_{i,j})^γ\]

where $β$ (human_exponent) and $γ$ (dist_exponent) are parameters. For each grid cell, a shortlist of size nshortlisted of the destination cells with the highest gravity are selected for use in the simulation.

The time taken for precalulation will depend on the scale argument. Values above 1 will downsample the grid to improve precalulation time and runtime performance. A high scale value is good for use in a live interface.

Keywords

• mode: Dispersal mode: Defaults to BatchGroups(), otherwise HeirarchicalGroups().
• human_pop: An array match the grid size containing human population data.
• cellsize: The size of the cell width, assuming they are square
• scale: Downscaling factor to reduce memory use and improve performance, defaults to 4 which means a 1:16 ratio.
• aggregator: a function that aggregates cells, defualting to mean.
• human_exponent: human population exponent.
• dist_exponent: distance exponent.
• dispersalperpop: sets the number of dispersing individuals from the origin as a proportion of the level of human activity.
• max_dispersers: maximum number of dispersers in a single dispersal event.
• nshortlisted: length of the dispersal destination shortlist for each cell. Longer lists are more accurate in the tail of the distribution, but are slower to access.

Pass grid Symbols to R or both R and W type parameters to use to specific grids.

populate!(A::AbstractMatrix, rule::HumanDispersal, [I...])
populate!(A::AbstractMatrix, cells::AbstractArray, [scale=1])

Populate a matrix with the precalculated destinations from a HumanDispersal rule - either all of the or some subset if passed the I... indexing arguments. This is useful for plotting dispersal destinations, especially when used with GeoData.jl

populate(rule::HumanDispersal, [I...])

Returns an array the size of human population matrix filled with all destination locataion, or with destinations specific to the passed-in indices I.

populate(cells::AbstractVector, size::Tuple, [scale::Int=1])

Returns an array of size size populated from the vector of positions in cells rescaled by scale.